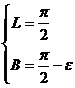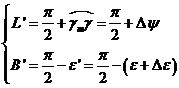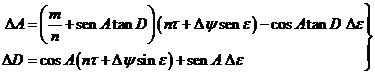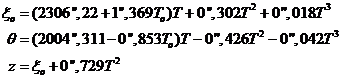2.8 Posiciones medias y verdaderas
Debido a la precesión, en
longitud y en oblicuidad, la eclíptica se desplaza girando y variando el ángulo
que forma con un plano fijo. Considerando únicamente estos movimientos
precesionales, obtenemos la eclíptica
media: plano definido por el centro del Sol, el centro de gravedad del
sistema Tierra‑Luna y la velocidad de este centro de gravedad.
Si corregimos de nutación la
eclíptica media, obtenemos la eclíptica
verdadera: plano determinado por el centro del Sol, el centro de la Tierra
y la velocidad de la Tierra.
También el ecuador experimenta
variaciones debidas a la precesión y nutación lunisolares. En cada instante
cabe considerar un ecuador verdadero,
que pasa por el centro de gravedad de la Tierra y es ortogonal al eje
instantáneo de rotación en dicho instante. Este plano se obtiene corrigiendo de
precesión y nutación.
Si sólo corregimos de precesión
obtenemos un ecuador medio.
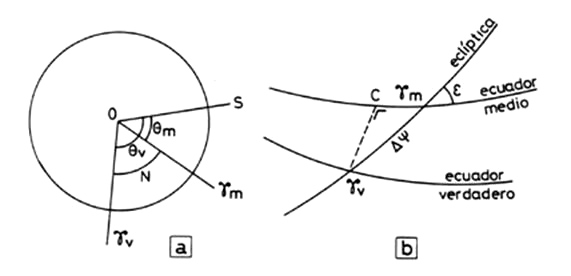
La intersección del ecuador medio
y la eclíptica media es la línea de los
equinoccios media y el nodo ascensional de la eclíptica es el punto Aries medio o equinoccio medio.
En cambio, si consideramos el
ecuador verdadero y la eclíptica verdadera, obtenemos el Aries verdadero o equinoccio
verdadero.
Se suelen considerar como
elementos de referencia medios los relativos al principio de un año astronómico. El año astronómico,
como veremos más adelante, empieza cuando la longitud media del Sol, corregida
de aberración, es igual a 280°. Se indica en la forma 1950,0 o 2.000,0.
El ángulo que forma el ecuador
medio con la eclíptica media en una fecha es la oblicuidad media en dicha fecha. La oblicuidad media de la
eclíptica, contada en años de 365,25 días a partir de la época J 2.000,0 vale:
e = 23º 26' 21",448 ‑ 0",46815 t ‑ 0",00000059 t2 + 0",00000000181 t3
(para la época actual t es negativo)
La oblicuidad verdadera en una fecha es el ángulo que forma la
eclíptica verdadera con el ecuador verdadero en dicha fecha.
Si referimos la posición de un
astro a la eclíptica y al equinoccio medios tenemos las coordenadas celestes medias del astro. De análoga forma se definen
las coordenadas celestes verdaderas.
Así, las coordenadas ecuatoriales medias
son las referidas al ecuador medio y las ecuatoriales
verdaderas las referidas al ecuador verdadero.
2.8.1 Variación de los polos celestes
A consecuencia de los movimientos
de precesión y de nutación el polo celeste se desplaza. Despreciemos la pequeña
variación secular de la oblicuidad de la eclíptica, es decir, consideremos que las
eclípticas verdadera y media coinciden. Debido a la precesión, el punto Aries
medio, gm retrograda a lo largo de
la eclíptica, por lo que, al ser la línea de los equinoccios media siempre
perpendicular al plano que determinan el centro de la esfera celeste, el polo
de la eclíptica Pe y el polo celeste medio Pm, el eje del
mundo describirá un cono de revolución alrededor del eje de la eclíptica, de
semiabertura igual a la oblicuidad de la eclíptica, en sentido retrógrado y
con una periodicidad de unos 26.000 años.
FIG 21.2
Debido a la nutación, el punto
Aries verdadero oscila a uno y otro lado del Aries medio y además, la
oblicuidad de la eclíptica varía periódicamente. En consecuencia, el polo
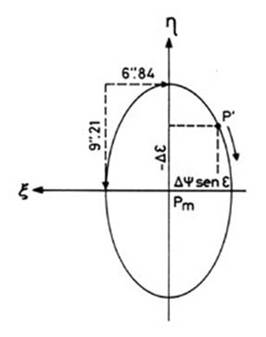
verdadero describe una pequeña elipse alrededor del polo medio; si nos
limitamos a su parte principal, los semiejes de dicha elipse son la constante
de la nutación 9",21 y 6",84.
Resumiendo: el eje del ecuador
medio describe un cono de revolución alrededor del eje de la eclíptica y el eje
verdadero un cono elíptico alrededor del eje medio (o lo que es lo mismo, el
polo del ecuador medio describe un círculo menor alrededor del polo de la
eclíptica y el polo verdadero una elipse alrededor del polo medio).
Estudiemos con detalle estos
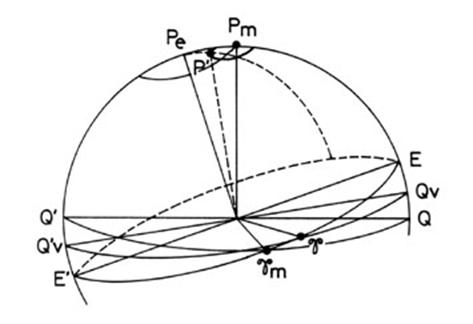
desplazamientos. En la Fig. 21.2 tenemos:
FIG 22.2
EE' eclíptica media de una época
QQ' ecuador medio de una época
QvQv’
ecuador verdadero de una época
Pe polo de la
eclíptica media
Pm polo del ecuador
verdadero
gm Aries medio
g Aries verdadero (aunque no lo hemos definido exactamente
así, consideraremos la intersección de la eclíptica media con el ecuador
verdadero dada la poca variación de la primera).
Consideremos las coordenadas
eclípticas de los polos ecuatoriales medio y verdadero:
|
Polo medio |
|
(63.2) |
|
Polo verdadero |
|
(64.2) |
donde Dy es la nutación en
longitud, e’ la oblicuidad verdadera y De la nutación en oblicuidad.
Estudiemos la variación del polo
verdadero en el plano tangente a la esfera celeste por el polo medio y en el
sistema de referencia (x,h) de la Fig.
22.2 El ángulo diedro formado por los máximos de longitud del polo medio y
del polo verdadero es L’‑L.
Debemos reducirlo al círculo menor multiplicando para ello por cos B. De (63.2) y (64.2) obtenemos:
Como que en latitud trabajamos
sobre un círculo máximo, no es necesario hacer ninguna reducción, y por tanto:
Por consiguiente, las coordenadas (x , h) del polo verdadero P'
en el sistema considerado serán:
(65.2)
Sabemos que los términos
principales de los efectos nutacionales causados por la Luna, son:
Sustituyendo en (65.2)
y refiriendo e a J 2.000,0 se tiene:
ecuaciones paramétricas de una elipse de semiejes
6",84 y 9",21. El eje mayor es el que tiene la dirección del máximo
de longitud. El periodo con que se realiza este movimiento es de 18 2/3 años.
Si tenemos en cuenta que el Aries
medio se mueve a lo largo de la eclíptica de modo que en un año retrograda de
50”,29, en el mismo intervalo de tiempo el polo medio se desplazará a lo largo
del círculo menor correspondiente de
Y así, mientras que en un año el polo medio se ha
desplazado 20”,0 sobre el eje x el polo verdadero habrá descrito
sólo una pequeña parte de la elipse, aproximadamente 1/18.
De acuerdo con lo que acabamos de
decir, la estrella polar no será siempre la misma. Todas las estrellas que
tengan una latitud de alrededor de 67º serán, alguna vez, polares en el
transcurso de unos 26.000 años. Actualmente la estrella polar es la a de la Osa Menor y su
distancia al polo es de alrededor de 1º. Esta distancia va disminuyendo en la
actualidad y alcanzará su valor mínimo en el año 2.105. Dentro de 12.000 años
la estrella polar será a Lirae (Vega), estrella de primera
magnitud Hace 6.000 años era g Draco, de tercera magnitud, que era la que
usaban como polar los astrónomos chinos.
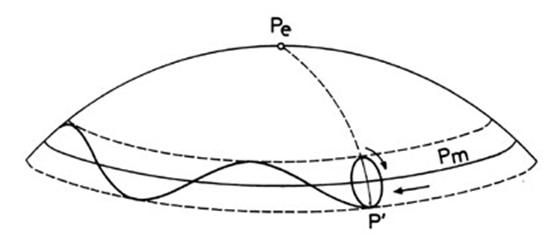
FIG 23.2
2.8.2 Corrección de precesión y nutación de las
coordenadas ecuatoriales
Los catálogos nos dan la posición
de los astros referida, usualmente, a la base media (ecuador y equinoccio
medios) del 1950,0 o del 2000,0. Si interesa conocer la posición media de la
fecha es necesario corregirla de precesión y, si lo que interesa obtener es la
posición verdadera (referida al ecuador y equinoccio verdaderos) deberemos
corregir además de nutación.
Para deducir la corrección
consideraremos, al igual que en el apartado anterior, que las eclípticas
verdadera y media coinciden y son fijas (realmente la eclíptica media varía muy
lentamente, con términos en t2
); por tanto, las latitudes de las estrellas se mantendrán invariables y sólo
deberán corregirse de precesión y nutación las longitudes:
(66.2)
donde las coordenadas B' y L' son las
verdaderas finales y las B y L las medias iniciales.
El término Dy es debido a la nutación y el
término pt a la precesión, siendo p la constante
de la precesión general en longitud:
p = 50'',2910 + 0'',000222
t
y t, medido en años, la fracción de
año transcurrida desde el comienzo del año astronómico en cuestión. El término precesional
es aditivo, pues al retrogradar Aries, aumenta la longitud de los astros.
Además, debido únicamente a la nutación, varía la oblicuidad de la eclíptica en
De.
Para hallar
partiremos de las ecuaciones (6.1) que nos dan el cambio de coordenadas eclípticas a
ecuatoriales:
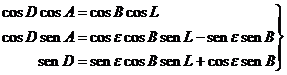
Diferenciando la tercera:
y teniendo en cuenta las otras dos:
y dividiendo ambos miembros por cos D, expresando las diferenciales por
incrementos:
(67.2)
Diferenciando ahora la primera:
sustituyendo dD
por (67.2) y operando:
Teniendo en cuenta la relación
y la ecuación del cambio de coordenadas inverso:
obtenemos:
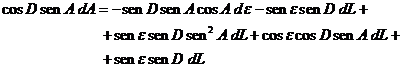
simplificando y haciendo igual que antes d=D
(68.2)
Teniendo en cuenta (66.2) e introduciendo para simplificar la precesión general en ascensión recta
y la precesión
general en declinación
(67.2) y (68.2)
pueden escribirse en la forma:
(69.2)
Introduzcamos ahora los llamados números de Bessel o besselianos que son
generales para toda la esfera celeste y vienen dados en los Anuarios día por
día:
y las constantes
estelares , dependientes de la estrella de que se trate
con lo que las fórmulas (69.2)
pueden escribirse en la forma:
(70.2)
Estas ecuaciones (70.2) nos permiten calcular las coordenadas verdaderas
(A',D') para una fecha dada, cuando se conocen las coordenadas medias (A,D)
para el principio del año.
Si quisiéramos obtener las
coordenadas medias de la fecha no consideraríamos los términos nutacionales:
obteniendo:
(71.2)
fórmulas que nos darían las posiciones medias de
la fecha a partir de las posiciones medias de principio de año.
Esta transformación se efectúa en
dos fases: recordemos que el catálogo de estrellas nos da las coordenadas
medias del comienzo de un año astronómico. Primero se obtienen las coordenadas
del principio del año astronómico en curso, o sea se hace la llamada reducción al año, y luego, a partir de
las coordenadas reducidas al año, se obtienen las coordenadas de la fecha o reducción al día (t es en este caso la fracción de año transcurrida desde el principio del año
astronómico).
Para obtener las posiciones
verdaderas de la fecha, se hallan las posiciones medias al principio del año
astronómico en curso (igual que en el caso anterior), reduciéndose
posteriormente al día, considerando ahora los términos nutacionales, mediante
las fórmulas (70.2).
Las fórmulas (71.2)
nos sirven también para hallar las coordenadas medias al principio de un año
conocidas las coordenadas medias al principio de un año anterior siendo ahora t el número de años
transcurridos (m y n están dados en los Anuarios y se toman para el año de
partida). Ahora bien, esto solamente es correcto si el intervalo de tiempo t es pequeño (poco menos de 5 años).
En la obtención de las posiciones
medias en una época T, conocidas las
posiciones medias en una época To
(reducción por precesión) suele emplearse otro método: sean 
las componentes del
vector de posición 
de un astro S en el sistema de coordenadas
ecuatoriales medias en la época T0,
(X0,Y0,Z0),
estando el eje X0 dirigido
hacia el punto Aries medio, el eje Z0
hacia el polo celeste medio P0
y el eje Y0 formando
triedro directo con los anteriores.
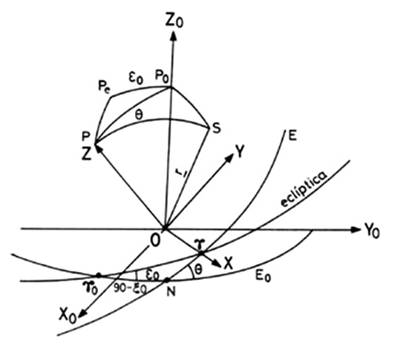
FIG 24.2
Consideremos, por otra parte, el
sistema de coordenadas ecuatoriales medias en la época T, (X,Y,Z) con el mismo
origen, y sean 
las componentes del vector de posición del
astro S en dicho sistema. El paso del
sistema X0,Y0, Z0
al X,Y,Z se realiza mediante tres
rotaciones, en función de los elementos precesionales x0,q ,z siendo 90°-x0 la ascensión recta del
nodo ascendente N del ecuador E de la época T sobre el ecuador E0
en la época T0 calculada
desde el equinoccio de T0,
q la inclinación del
ecuador en la época T sobre el
ecuador en la época T0 y
90º+z la ascensión recta del nodo
contada desde el equinoccio de T. De
modo que:
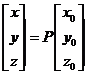
donde la matriz
de precesión P es
P = R3(-90º-z) R1(q) R3(90º-x0)
cuyos elementos son:
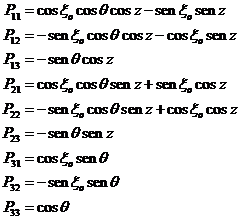(72.2)
estando los parámetros x0, q y z
definidos por:
(73.2)
Para su cálculo se han tenido en
cuenta las constantes astronómicas del sistema IAU(1976) y están referidos a la
época J 2000,0. T0 es la
fracción de siglo del catálogo inicial y T
es la fracción de siglo transcurrida desde el año a que está referido el
catálogo. En el caso particular de tomar como época inicial el año J 2000,0 (lo
que sucederá al utilizar el catálogo fundamental FK5), deberán usarse las
expresiones que resulten de hacer T0
= 0 en las (73.2) donde T será el número de siglos julianos de 36525 días que separan la
fecha en cuestión del año J 2000,0 cuya fecha juliana correspondiente es
2451545,0 y que equivale a 2000 enero 1,5.
Los valores numéricos de los
elementos de la matriz de precesión han sido calculados, para pasar de T0=B 1950,0 a T= J 2000,0 ,
entre otros autores por J.H. Lieske (1979), obteniendo:
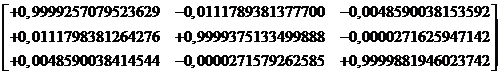
En enero de 1998 la Unión
Astronómica Internacional (IAU) adoptó el nuevo sistema de referencia ICRS
(Internacional Celestial Reference System). Como consecuencia de ello,
actualmente los elementos de esta matriz de precesión están siendo revisados
por varios autores.
Según vimos en el primer capítulo
(1.5), la ecuación de equinoccios es:
N = qV - qm
Es decir, proyectando sobre el
ecuador (Fig. 25.2) vemos que representa la nutación en
ascensión recta, puesto que, la ascensión recta del Aries medio es cero,
mientras que la del Aries verdadero es N.
FIG 25.2
Si consideramos como plano el
triángulo gV gm C de la Fig.
25.2 b) teniendo en cuenta que Dy es muy pequeño:
N = Dy cos e
y tomando en Dy el término de mayor contribución:
que implica que la parte principal de la ecuación
de equinoccios oscila con una periodicidad de 18,6 años y una amplitud de algo
más de 1s.