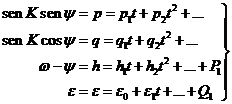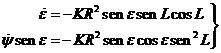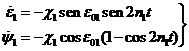2.7 Precesión y Nutación
2.7.1 Movimientos de los planos fundamentales
a los que se refieren las coordenadas de los astros
La
acción perturbatriz del Sol, la Luna y los planetas sobre la Tierra da lugar a
que, en el transcurso del tiempo, cambien de posición en el espacio los planos
fundamentales, eclíptica y ecuador, definidos por los movimientos de traslación
y rotación de la Tierra con respecto a un sistema de referencia fijo.
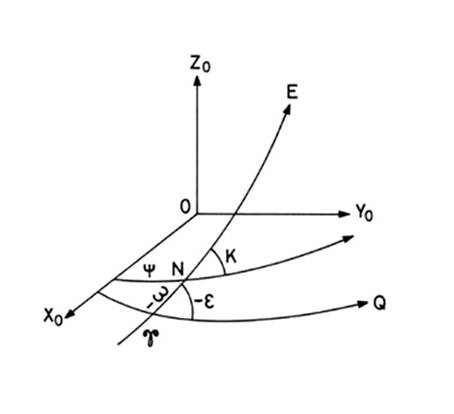
Para
definir las posiciones de la eclíptica E
y el ecuador Q en una cierta época,
suelen referirse éstos a un plano de referencia xo yo y una dirección origen en él (que puede
ser, por ejemplo, la eclíptica y el punto Aries en una época determinada)
dando la longitud del nodo y y la inclinación K de E
respecto a xo yo,
y la longitud del nodo ‑w y la inclinación ‑e
de Q con respecto a E (Fig. 18.2).
FIG 18.2
La
teoría del movimiento de traslación de la Tierra alrededor del Sol suministra y y
K por las relaciones
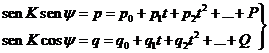
cuyos segundos miembros
constan de una parte de variación secular, en potencias crecientes de t, y de otra parte periódica P y Q.
Asimismo,
la teoría del movimiento de rotación de la Tierra suministra directamente w-y y
e en la forma:
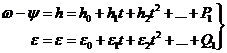
cuyos segundos miembros
constan también de una parte secular y una parte periódica P1 y Q1.
Tomando
como plano de referencia x0 y0
el de la eclíptica E0 en la época en que se empieza a contar el tiempo,
y despreciando los términos periódicos P y Q, dada su pequeñez, las relaciones
anteriores toman la forma:
(59.2)
ya que, en efecto, ello equivale
a hacer K=0, sen K=0 y para t=0,
despreciando P y Q, queda p0=0,
q0=0, siendo además, para t=0, w=y y
por tanto, también, h0=0.
En
términos generales, recibe el nombre de precesión
las variaciones de la eclíptica, el ecuador y el equinoccio representadas por
los términos seculares de (59.2) y el de nutación
las variaciones de la eclíptica, el ecuador y el equinoccio representadas por
los términos periódicos P1 y Q1.
En
particular, los términos seculares de h
reciben el nombre de precesión general
en longitud y los de e
la denominación de oblicuidad media de la
eclíptica. El coeficiente h1
es la constante de precesión general en
longitud y su valor por siglo juliano en la época J 2000,0 es h =
5029",0966. El valor de e0
en la época J 2000,0 es e0 = 23º 26' 21",448.
Los
términos periódicos P1 y Q1 se denominan,
respectivamente, nutación en longitud
y nutación en oblicuidad.
2.7.2 Precesión y nutación solares
Como
hemos indicado, la precesión y la nutación son debidas a la acción que sobre la
Tierra producen los momentos de los astros perturbadores. Pueden ser de
origen solar, lunar o planetario.
Estudiaremos en primer lugar la precesión y la nutación de origen solar.
FIG 19.2
Consideraremos un sol ficticio " que describa la
eclíptica con velocidad angular n constante y con un radio R igual a la
distancia media de la Tierra al Sol:
La longitud L de este sol ficticio crece proporcionalmente al tiempo, siendo L = nt si empezamos a contar el tiempo
cuando el Sol pasa por el punto Aries.
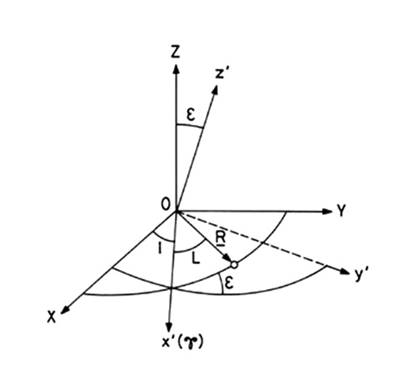
Consideremos dos sistemas de
coordenadas cartesianas rectangulares con, origen común en el centro de
gravedad de la Tierra: X,Y,Z tal que el plano fundamental X,Y sea el plano de
la eclíptica y Z en la dirección del polo de la eclíptica; x',y',z' tal que x',y'
sea el plano del ecuador, con x' hacia el punto Aries (Fig.
19.2), los dos orientados en sentido directo. Las coordenadas ecuatoriales
del Sol son:
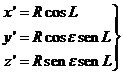(60.2)
Sustituyéndolas en las relaciones
(58.2) del apartado 2.6.1
teniendo en cuenta que ahora q =‑e, tendremos:
(61.2)
Como que e varía muy lentamente podemos
considerarla constante (=e0) en los segundos miembros de (61.2)
y con L=nt
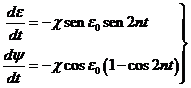
donde
(m=masa
del Sol)
Al integrar tendremos:
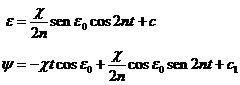
Con c1=y0.
Observemos que e, oblicuidad de la
eclíptica, varía periódicamente con un periodo de medio año (T=365,25/2 , ya que 2n=2p/T)
El término 
recibe el nombre de nutación en oblicuidad.
En y aparece un término lineal en t que es la precesión en longitud y uno periódico que es la nutación en longitud. Esto implica que, con
el tiempo, el punto Aries va retrogradando sobre la eclíptica, ya que el
coeficiente del término secular es negativo, y que al mismo tiempo que
retrograda, va oscilando alrededor del Aries
medio que es el obtenido teniendo en cuenta sólo la precesión en longitud.
Naturalmente las hipótesis
admitidas de que la distancia R del
Sol a la Tierra permanece constante, como también que la longitud L del Sol varía uniformemente con el
tiempo, están muy lejos de la realidad, y ello hace que la nutación debida a la
atracción solar no quede perfectamente expresada por los términos 
. A estos términos es preciso agregarles otros, también de
carácter periódico, en que intervendrá la posición del Sol respecto al apogeo;
términos que, aunque de menor importancia que los citados, no son completamente
despreciables.
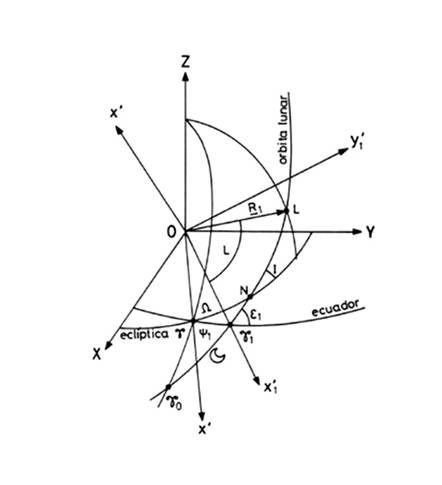
2.7.3 Precesión y nutación lunares
La Luna sigue una órbita media
con una inclinación I respecto a la
eclíptica que oscila entre 5º y 5º 18', es decir, en media I=5º 9'. Se denomina línea de
los nodos a la intersección del plano de la órbita lunar con el plano de
la eclíptica. Al punto N por el cual
la Luna pasa del hemisferio celeste sur al hemisferio celeste norte se le llama
nodo ascendente y al punto
diametralmente opuesto nodo descendente.
En primera aproximación, la
órbita de la Luna es una elipse con una excentricidad del orden de 1/20. Supongamos
que es una circunferencia de radio R1
igual a la distancia media de la Tierra a la Luna, recorrida con velocidad
media constante n1:
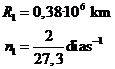
Procederemos análogamente al
apartado anterior, tomando como plano x,y
el del ecuador (que llamaremos x', y') y como plano x', y' el de la órbita lunar (que llamaremos x1', y1') con x1' dirigido hacia 1a intersección de la órbita lunar
con el ecuador, g1. Si R1 es el radio vector de la Luna, L, los ángulos de Euler serán (Fig. 20.2):
FIG 20.2
y = y1 medido sobre el ecuador
q = -e1
j = L1 = 
medido sobre la órbita lunar
La longitud media de la Luna crece
proporcionalmente al tiempo, siendo L1
= n1t si empezamos a contar el tiempo cuando la Luna pasa por g1.
Estamos pues en una situación
completamente paralela a la del apartado anterior, por lo que sustituyendo en
las mismas fórmulas (58.2) obtendremos:
(62.2)
con
siendo la razón entre c1 y c
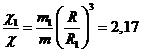
Integrando
(62.2) obtendremos:
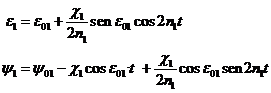
fórmulas que suelen darse en función de W y V siendo (Fig.
20.2)
= longitud del nodo lunar
(t
en años)
= longitud de la Luna sobre su órbita = 
(t en días)
E1 nodo ascendente retrograda a
lo largo de la eclíptica dando una vuelta completa en 18,6 años, fenómeno que
recibe el nombre de retrogradación de la
línea de los nodos de la órbita lunar y es debido a las perturbaciones
gravitatorias que ejerce la Tierra sobre la Luna.
Al poner L1=n1t en función de W y V se obtiene en e1 una suma de términos
periódicos (cosW, cos2W, cos2V ) que constituyen la nutación lunar en oblicuidad. En y1 se obtiene un término
secular en t, la precesión lunar en longitud y una suma de términos periódicos (senW, sen2V, sen2W ), la
nutación lunar en longitud.
2.7.4 Precesión y nutación luni‑solares
Como su nombre indica, son
debidas a la acción gravitatoria combinada del Sol y la Luna. Se obtienen sumando
término a término (precesión con precesión, nutación con nutación) las
precesiones y nutaciones solar y lunar:
yLS = y + y1 precesión y nutación
luni-solar en longitud.
eLS = e + e1 nutación luni-solar en
oblicuidad.
obteniéndose:
donde t
viene dado en años de 365,25 días.
Al factor 50",39 se le llama
constante de la precesión luni‑solar
y al factor 9",21 constante de la
nutación (no se especifica que sea luni‑solar dado que es el término
nutacional en oblicuidad más importante de todos los que seguirán).
2.7.5 Precesión y nutación planetarias
Los planetas, en especial Júpiter
(por su masa) y Venus (por su proximidad), producen un avance del punto Aries
de 0",11 por año, precesión
planetaria en longitud. Además, aparece una precesión planetaria en
oblicuidad de ‑0",47 t +
... que corresponde, realmente, al primer término del desarrollo en serie de
una nutación de periodo muy largo (40.000 años). También aparecen términos
nutacionales en G y G’ (longitudes de los
perigeos solar y lunar, respectivamente). Como era de esperar, los efectos son
mucho menores que los debidos al Sol y la Luna.
2.7.6 Precesión y nutación generales
Son debidas a la composición de
todos los efectos anteriormente estudiados:
y = y0 - 50",29 t + …+ (términos nutacionales)
e = eo ‑ 0",46815 t ‑ 0",00000059 t2 + ... + (términos
nutacionales)
Al término secular en longitud ‑50",29
se le llama constante de la precesión
general. Implica que el punto Aries retrograda sobre la eclíptica a razón
de 50",29 por año, recorriéndola, por tanto, aproximadamente, en unos
26.000 años.
Existe una corrección relativista
de la precesión en longitud de +0",02 por año, que se considera englobada
en la luni‑solar.
Por otra parte, el suponer
constantes e y e1 en los segundos miembros de las
ecuaciones diferenciales, se ha introducido un error que provoca que las
constantes de precesión y nutación no sean realmente constantes. Teniendo en
cuenta este hecho, tales "constantes" valen para la época J 2.000,0:
constante de la precesión general = 50",291 + 0",00022
t
constante de la nutación = 9",206 + 0",000009 t
(t en años de 365,25 días).