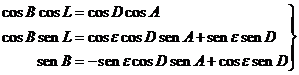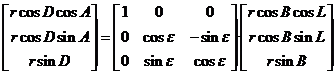1.4 Coordenadas ecuatoriales y eclípticas

En los sistemas de coordenadas ecuatoriales (o uranográficas) y eclípticas los triedros de referencia están orientados en sentido directo y son solidarios a la esfera celeste.

1.4.1 Coordenadas ecuatoriales

En el sistema de coordenadas ecuatoriales se define el triedro de referencia tomando como eje x la dirección de la línea de los equinoccios, en sentido positivo hacia el punto Aries, el eje y situado sobre el ecuador, a 90° del anterior, en sentido directo y el eje z en la dirección del eje del mundo y en sentido positivo hacia el polo celeste norte.

Las componentes del vector de posición de un astro E en dicha base constituyen las coordenadas ecuatoriales rectilíneas del mismo E(x, y, z).

Un punto de la esfera celeste, distinto de los polos, también queda completamente determinado por un único meridiano y un único paralelo celestes, que permiten definir las coordenadas ecuatoriales esféricas (Fig.9.1)

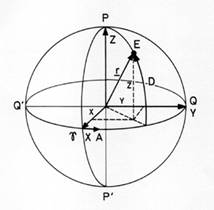
FIG 9.1

Ascensión recta, A, es el ángulo diedro que forman el plano meridiano que pasa por el astro y el coluro de los equinoccios. Se mide en tiempo, sobre el ecuador, desde el punto Aries hasta el pie del meridiano que pasa por el astro, en sentido directo de 0 h a 24 h:

Declinación, D, es la distancia esférica desde el ecuador hasta el paralelo que pasa por el astro. Se mide en grados desde el ecuador, de 0° a 90°; es positiva si el astro se encuentra en el hemisferio celeste norte y negativa si en el sur:

Distancia, r, es el módulo del vector de posición.

Distancia polar, p, es la distancia esférica del polo celeste norte al astro:

Las relaciones entre las coordenadas ecuatoriales rectilíneas y esféricas vienen dadas por (Fig. 9.1):

1.4.2 Coordenadas eclípticas

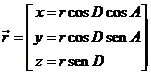
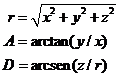
En el sistema de coordenadas eclípticas definiremos el triedro de referencia tomando el eje x' idéntico al anterior x, el eje y' en la dirección de la línea de los solsticios, sentido positivo hacia el punto de Cáncer, y el eje z' en la dirección del eje de la eclíptica, en sentido positivo hacia el polo eclíptico norte.

Las componentes del vector de posición del astro E en dicha base constituyen las coordenadas eclípticas rectilíneas E(x', y', z').

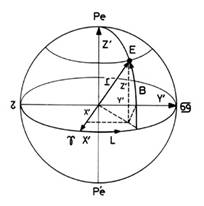
FIG 10.1

Por cada punto de la esfera celeste, distinto de los polos eclípticos, pasan un único máximo de longitud y un único menor de latitud que nos permiten definir las coordenadas eclípticas esféricas (Fig.10.1).

Longitud celeste, L, es el ángulo diedro que forman el máximo de longitud que pasa por el astro y el máximo de longitud que pasa por el punto Aries, contado a partir del punto Aries, sobre la eclíptica, en sentido directo, de 0° a 360°:

Latitud celeste, B, es la distancia esférica desde la eclíptica hasta el menor de latitud que pasa por el astro. Se mide en grados y es positiva si el astro se encuentra en el hemisferio norte y negativa si en el sur:

Distancia, r, es el radio de la esfera celeste.

Las relaciones entre las coordenadas eclípticas rectilíneas y esféricas son (Fig.10.1):

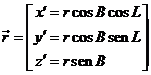
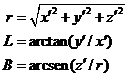
1.4.3 Paso de coordenadas ecuatoriales a eclípticas y viceversa

Los triedros de referencia de los sistemas de coordenadas ecuatoriales y eclípticas tienen común el eje x, y ambos están orientados en sentido directo, por lo que podrá efectuarse el cambio de un sistema al otro por una simple rotación R₁ alrededor del eje x de ángulo e o -e (Fig. 11.1).

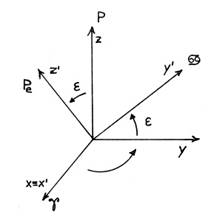
FIG 11.1

Si queremos pasar de coordenadas ecuatoriales a eclípticas, procediendo de manera análoga a como hicimos en la sección 1.2.3, tendremos:

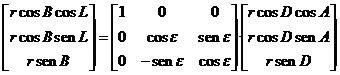
es decir:

(5.1)

El cambio inverso será:

es decir:

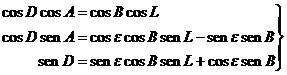(6.1)

Estas fórmulas (5.1) y (6.1) también pueden obtenerse aplicando el grupo de Bessel al triángulo polo del ecuador‑polo de la eclíptica‑astro.

1.4.4 Variación de las coordenadas del Sol en su movimiento ánuo

De acuerdo con la ley de las áreas de Kepler, aunque la longitud aparente del Sol sea siempre creciente, su variación no es uniforme. Si consideramos que el Sol, S, describe la eclíptica, B es nula; las demás coordenadas varían según la tabla adjunta obtenida al resolver el triángulo donde = longitud, = ascensión recta y = declinación (Fig. 12.1).

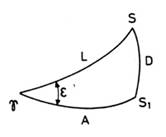
FIG 12.1

TABLA I

Situación del Sol	L	A	D
	0^o	0^h	0^o
a	90^o	6^h	+e
d	180^o	12^h	0^o
g	270^o	18^h	-e
	360^o	24^h	0^o

Se observa que A es siempre creciente y D toma sus valores máximo y mínimo en los puntos Cáncer y Capricornio, respectivamente.

En un día las variaciones de A y de D son pequeñas,

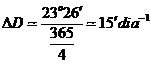
suponiendo el movimiento uniforme, por lo que en muchas aplicaciones, a lo largo de un día, tanto la ascensión recta como la declinación pueden considerarse constantes e iguales a su valor medio en dicho día.

Del mismo triángulo (Fig.12.1)determinado por la posición del Sol, S, el punto Aries, , y la intersección del meridiano celeste que pasa por el centro del Sol con el ecuador, S₁, deducimos también las relaciones:

ANTERIOR

ÍNDICE

SIGUIENTE