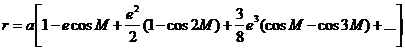3.7 Desarrollos en
serie
Obtendremos ahora los desarrollos en serie de
las anomalías excéntrica y verdadera y del radio vector en función de la
anomalía media y la excentricidad.
3.7.1 Desarrollo en serie de la anomalía excéntrica
Expresaremos E por desarrollo en serie de Mac-Laurin
de potencias de e, considerando M como parámetro. Para hallar los
distintos términos del mismo, derivaremos sucesivamente la ecuación de Kepler:
![]()
![]()
![]()
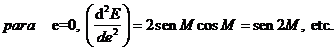
y aplicando la fórmula de Mac-Laurin:
3.7.2 Desarrollo en serie del radio vector
Derivando la ecuación de Kepler
y recordando la expresión del radio vector
r=a(l-ecos E),
obtenemos:
![]()
y de aquí:
![]()
Calcularemos
![]() a partir de (47.3), considerando e constante:
a partir de (47.3), considerando e constante:
de donde, desarrollando en serie por división:
3.7.3 Desarrollo en serie de la anomalía verdadera
Teniendo en cuenta la ley de las áreas:
![]()
y que
![]()
sustituyendo dt y despejando dV, se deduce:
![]()
De (48.3) se obtiene,
elevando al cuadrado y ordenando según las potencias de e:
![]()
y desarrollando![]() :
:
![]()
Multiplicando estas dos series se obtiene:
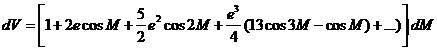
e integrando y observando que para V=0, M=0
(por lo que la constante de integración será nula), finalmente:
![]() (50.3)
(50.3)
3.7.4 Desarrollo en serie de las coordenadas reducidas
Hemos definido como coordenadas reducidas
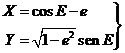
Recordando una vez más que r=a(l-ecosE),
despejando cosE
y teniendo en cuenta (49.3):
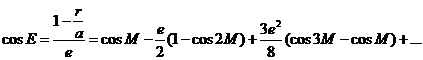
y restando e
de esta última expresión:
![]() (51.3)
(51.3)
Por otra parte, de la ecuación de Kepler, despejando senE y teniendo en cuenta (47.3):
![]()
y multiplicando por el desarrollo de ![]() obtenido
anteriormente:
obtenido
anteriormente:
![]() (52.3)
(52.3)